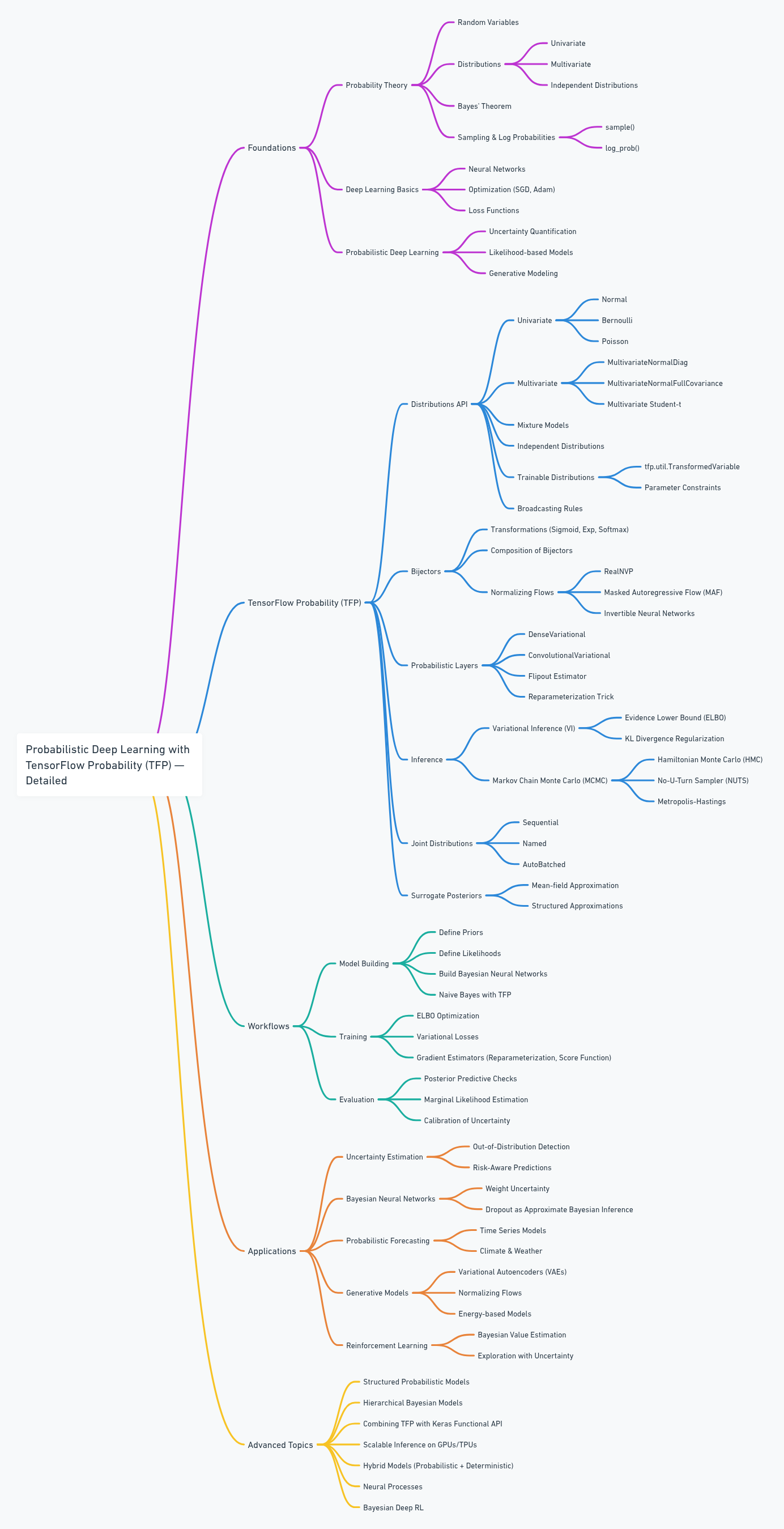
This repository is a comprehensive collection of TensorFlow Probability implementations for probabilistic deep learning. The primary goal is educational: to bridge the gap between traditional deterministic models and real-world uncertainty quantification.
✨Unlock the power of uncertainty quantification in machine learning.
This repository provides hands-on implementations of probabilistic deep learning using TensorFlow Probability (TFP), enabling you to build models that not only make predictions but also quantify how confident they are about those predictions.
Documentation: TFP API Docs
Traditional machine learning models provide point estimates without quantifying uncertainty. In critical applications like medical diagnosis, autonomous vehicles, or financial modeling, knowing how confident your model is can be the difference between success and catastrophic failure.
-
Enables models to express confidence levels using probabilistic layers and Bayesian neural networks.
-
Supports sampling, log-likelihood evaluation, and manipulation of complex distributions (univariate & multivariate).
-
Powers VAEs and normalizing flows for density estimation, representation learning, and synthetic data generation.
This repository demonstrates how TensorFlow Probability transforms your standard neural networks into probabilistic powerhouses that:
- Quantify uncertainty in predictions
- Model complex distributions beyond simple Gaussian assumptions
- Perform Bayesian inference at scale
- Generate realistic synthetic data through advanced generative models
Real-world data is messy, incomplete, and uncertain. Probabilistic deep learning addresses these challenges by:
- Handling Data Scarcity: Bayesian approaches work well with limited data.
- Robust Decision Making: Uncertainty estimates guide better decisions.
- Interpretable AI: Understanding model confidence builds trust
- Anomaly Detection: Identifying outliers and unusual patterns.
- Risk Assessment: Quantifying potential failure modes.
-
Bayesian neural networks: Adds priors to weights and calibrates predictive uncertainty for out-of-distribution robustness.
-
Normalizing flows: Uses invertible transforms for expressive density estimation and efficient sampling.
-
Variational inference: Optimizes ELBO with reparameterization for controllable generation and learning.
- Higher memory and training time than deterministic models.
- Gains in interpretability, calibrated risk, and anomaly detection often outweigh the cost
- Linear Algebra: Matrix operations, eigenvalues, SVD
- Calculus: Derivatives, gradients, optimization
- Statistics: Probability theory, Bayes' theorem, distributions
- Information Theory: KL divergence, entropy, mutual information
- Python 3.8+ with object-oriented programming
- TensorFlow/Keras fundamentals
- NumPy/SciPy for numerical computing
- Matplotlib/Seaborn for visualization
- Pattern Recognition and Machine Learning by Christopher Bishop
- The Elements of Statistical Learning by Hastie, Tibshirani, and Friedman
- Probabilistic Machine Learning by Kevin Murphy
-
Clone the repository:
git clone https://github.com/mohd-faizy/Probabilistic-Deep-Learning-with-TensorFlow.git cd Probabilistic-Deep-Learning-with-TensorFlow -
Create virtual environment (using uv – ⚡ faster alternative):
# Install uv if not already installed pip install uv # Create and activate virtual environment uv venv # Activate the env source .venv/bin/activate # Linux/macOS .venv\Scripts\activate # Windows
-
Install dependencies:
uv add -r requirements.txt
-
Verify installation:
import tensorflow as tf import tensorflow_probability as tfp print(f"TensorFlow: {tf.__version__}") print(f"TensorFlow Probability: {tfp.__version__}")
import tensorflow as tf
import tensorflow_probability as tfp
tfd = tfp.distributions
# Create a probabilistic model
def create_bayesian_model():
model = tf.keras.Sequential([
tfp.layers.DenseVariational(
units=64,
make_prior_fn=lambda: tfd.Normal(0., 1.),
make_posterior_fn=tfp.layers.default_mean_field_normal_fn(),
kl_weight=1/50000
),
tf.keras.layers.Dense(10, activation='softmax')
])
return model
# Train with uncertainty quantification
model = create_bayesian_model()
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy')Understanding these distributions is crucial for effective probabilistic modeling:
Models the number of successes in (n) independent trials with probability (p).
Use Cases: A/B testing, quality control, medical trials
Models the number of events occurring in a fixed interval.
Use Cases: Customer arrivals, system failures, web traffic
The cornerstone of probabilistic modeling with symmetric, bell-shaped curves.
Use Cases: Neural network weights, measurement errors, natural phenomena
Models waiting times and survival analysis.
Use Cases: System reliability, queueing theory, survival analysis
Essential for modeling correlated variables with full covariance structure.
Use Cases: Dimensionality reduction, portfolio optimization, computer vision
| Model Type | Dataset | Standard NN | Bayesian NN | VAE | Normalizing Flow |
|---|---|---|---|---|---|
| MNIST Classification | 60k samples | 2 min | 8 min | 12 min | 15 min |
| CIFAR-10 Classification | 50k samples | 15 min | 45 min | 60 min | 90 min |
| CelebA Generation | 200k samples | N/A | N/A | 120 min | 180 min |
Benchmarks on NVIDIA RTX 3080 GPU
Probabilistic models typically require 2-4x more memory than standard models due to:
- Parameter uncertainty representation
- Additional forward/backward passes
- Sampling operations during training
| Aspect | TensorFlow Probability (TFP) | TensorFlow Core (TF) |
|---|---|---|
| Primary Focus | Probabilistic modeling, uncertainty quantification | Deterministic neural networks, optimization |
| Model Output | Distributions with uncertainty bounds | Point estimates |
| Key Strengths | Bayesian inference, generative modeling | Fast training, established workflows |
| Learning Curve | Steeper (requires probability theory) | Gentler (standard ML concepts) |
| Memory Usage | Higher (parameter distributions) | Lower (point parameters) |
| Training Time | Slower (sampling, variational inference) | Faster (direct optimization) |
| Interpretability | Higher (uncertainty quantification) | Lower (black box predictions) |
| Best Use Cases | Critical decisions, small data, research | Large datasets, production systems |
We welcome contributions from the community! Here's how you can help:
- Fork the repository
- Create a feature branch (
git checkout -b feature/amazing-feature) - Commit your changes (
git commit -m 'Add amazing feature') - Push to the branch (
git push origin feature/amazing-feature) - Open a Pull Request
- Auto-Encoding Variational Bayes - Kingma & Welling (2013)
- Stochastic Backpropagation and Approximate Inference in Deep Generative Models - Rezende et al. (2014)
- Weight Uncertainty in Neural Networks - Blundell et al. (2015)
- Variational Inference: A Review for Statisticians - Blei et al. (2017)
- Probabilistic Machine Learning and Artificial Intelligence - Ghahramani (2015)
- Normalizing Flows for Probabilistic Modeling and Inference - Papamakarios et al. (2019)
- Density estimation using Real NVP - Dinh et al. (2016)
- Glow: Generative Flow with Invertible 1x1 Convolutions - Kingma & Dhariwal (2018)
- Practical Variational Inference for Neural Networks - Graves (2011)
- What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision? - Kendall & Gal (2017)
- Simple and Scalable Predictive Uncertainty Estimation using Deep Ensembles - Lakshminarayanan et al. (2017)
- Black Box Variational Inference - Ranganath et al. (2014)
- Automatic Differentiation Variational Inference - Kucukelbir et al. (2017)
- The No-U-Turn Sampler: Adaptively Setting Path Lengths in Hamiltonian Monte Carlo - Hoffman & Gelman (2014)
- TensorFlow Distributions - Dillon et al. (2017)
- Probabilistic Programming and Bayesian Methods for Hackers - Davidson-Pilon (2015)
- Leveraging Heteroscedastic Aleatoric Uncertainties for Robust Real-Time LiDAR 3D Object Detection - Chang et al. (2020)
- Predictive Uncertainty Estimation via Prior Networks - Malinin & Gales (2018)
This project is licensed under the MIT License - see the LICENSE file for details