TOGO - Basic 2D geometric operations

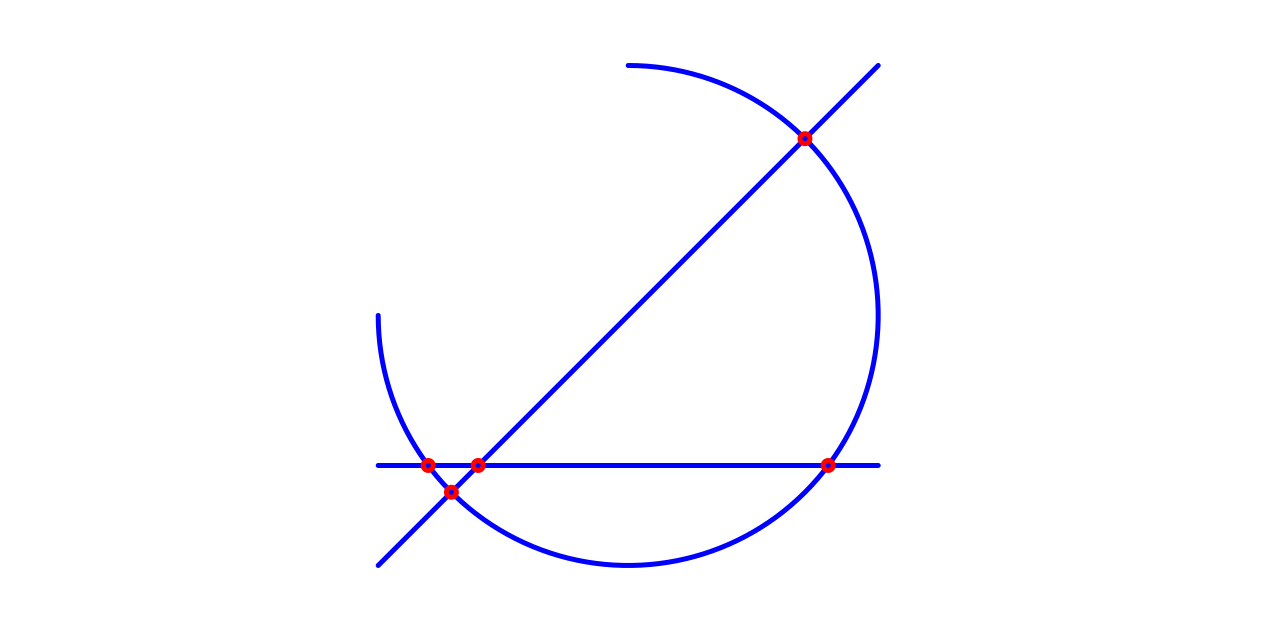
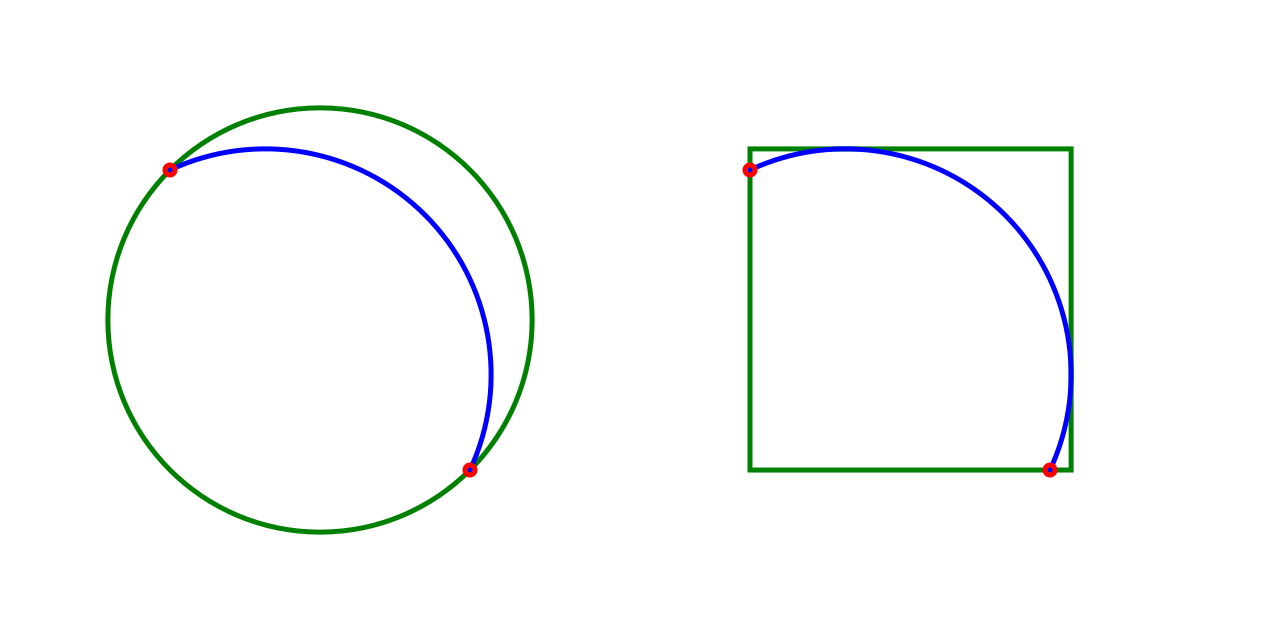
This library provides 2D geometric operations for arcs and line segments. It is used in my other projects and may not implement all possible geometric operations.

Adding the library to Cargo.toml

[dependencies]
togo = "0.5"

Documentation

https://docs.rs/togo

Core Capabilities

2D Geometric Primitives: Points, Line Segments, Circles, Circle Arcs, Polylines, Intervals

Distance Calculations: point-arc, point-circle, point-segment, segment-arc, segment-circle, segment-segment, line-circle, arc-arc

Intersection Detection: line-line, line-circle, line-arc, circle-circle, segment-segment, segment-circle, segment-arc, arc-arc, interval-interval

Geometric Algorithms: Convex Hull, Convexity Detection, Area Calculations (point/arc-based), Bounding Circle/Rectangle

Numerical Operations: Vector arithmetic (add, sub, mul, div), dot/cross product, normalization, point equality (ULP & epsilon-based)

Examples

Important

Arcs are always CCW (counter-clockwise) in this library.

Working with geometric primitives and distances

use togo::prelude::*;

// Create primitives: points, circle, segment, arc
let p1 = point(0.0, 0.0);
let p2 = point(10.0, 0.0);
let c = circle(p1, 5.0);
let seg = segment(p1, p2);
let arc = arc(point(1.0, 0.0), point(0.0, 1.0), point(0.0, 0.0), 1.0);

// Compute distances
let (dist, _) = dist_point_circle(&point(10.0, 0.0), &c);
assert_eq!(dist, 5.0);

let (dist, _) = dist_point_segment(&point(5.0, 5.0), &seg);
assert_eq!(dist, 5.0);

// Distance between arcs
let a2 = arc(point(4.0, 0.0), point(2.0, 0.0), point(3.0, 0.0), 1.0);
let dist = dist_arc_arc(&arc, &a2);
assert!(dist > 0.0);

Intersection computations

use togo::prelude::*;

// Segment-segment intersection
let seg1 = segment(point(0.0, 0.0), point(2.0, 2.0));
let seg2 = segment(point(0.0, 2.0), point(2.0, 0.0));
match int_segment_segment(&seg1, &seg2) {
    SegmentSegmentConfig::OnePoint(pt, ..) => {
        assert!(point(1.0, 1.0).close_enough(pt, 1e-10));
    },
    _ => assert!(false, "Expected intersection"),
}

// Circle-circle intersection
let c1 = circle(point(0.0, 0.0), 3.0);
let c2 = circle(point(4.0, 0.0), 3.0);
match int_circle_circle(c1, c2) {
    CircleCircleConfig::NoncocircularTwoPoints(_, _) => {
        assert!(true); // Two intersection points found
    },
    _ => assert!(false, "Expected two intersection points"),
}

// Arc-arc intersection
let a1 = arc(point(1.0, 0.0), point(0.0, 1.0), point(0.0, 0.0), 1.0);
let a2 = arc(point(1.0, 1.0), point(0.0, 0.0), point(1.0, 0.0), 1.0);
match int_arc_arc(&a1, &a2) {
    ArcArcConfig::NonCocircularOnePoint(pt) => {
        assert_eq!(point(0.5, 0.8660254037844386), pt);
    },
    _ => assert!(false, "Expected one intersection point"),
}

Algorithms: Area, Convex Hull, Bounding

use togo::prelude::*;
use togo::algo::{pointline_area, pointline_convex_hull, arc_bounding_circle};

// Calculate area of a polygon
let triangle = vec![point(0.0, 0.0), point(4.0, 0.0), point(2.0, 3.0), point(0.0, 0.0)];
let area = pointline_area(&triangle);
assert_eq!(area, 6.0);

// Find convex hull
let points = vec![
    point(0.0, 0.0),
    point(2.0, 1.0),
    point(1.0, 2.0),    // Interior (excluded)
    point(3.0, 0.0),
    point(2.0, 3.0),
    point(0.0, 2.0),
];
let hull = pointline_convex_hull(&points);
assert_eq!(hull.len(), 4);  // 4 points on convex hull

// Bounding circle for an arc
let quarter_arc = arc(point(1.0, 0.0), point(0.0, 1.0), point(0.0, 0.0), 1.0);
let bounding = arc_bounding_circle(&quarter_arc);
assert_eq!(bounding.r, 0.7071067811865476); // sqrt(2)/2